[백준] 11729-하노이 탑 이동순서-Java
in Algorithm on Algorithm
[백준] 11729-하노이 탑 이동순서-Java
🖊️풀이법
하노이탑의 핵심 개념을 한번 먼저 살펴보자.
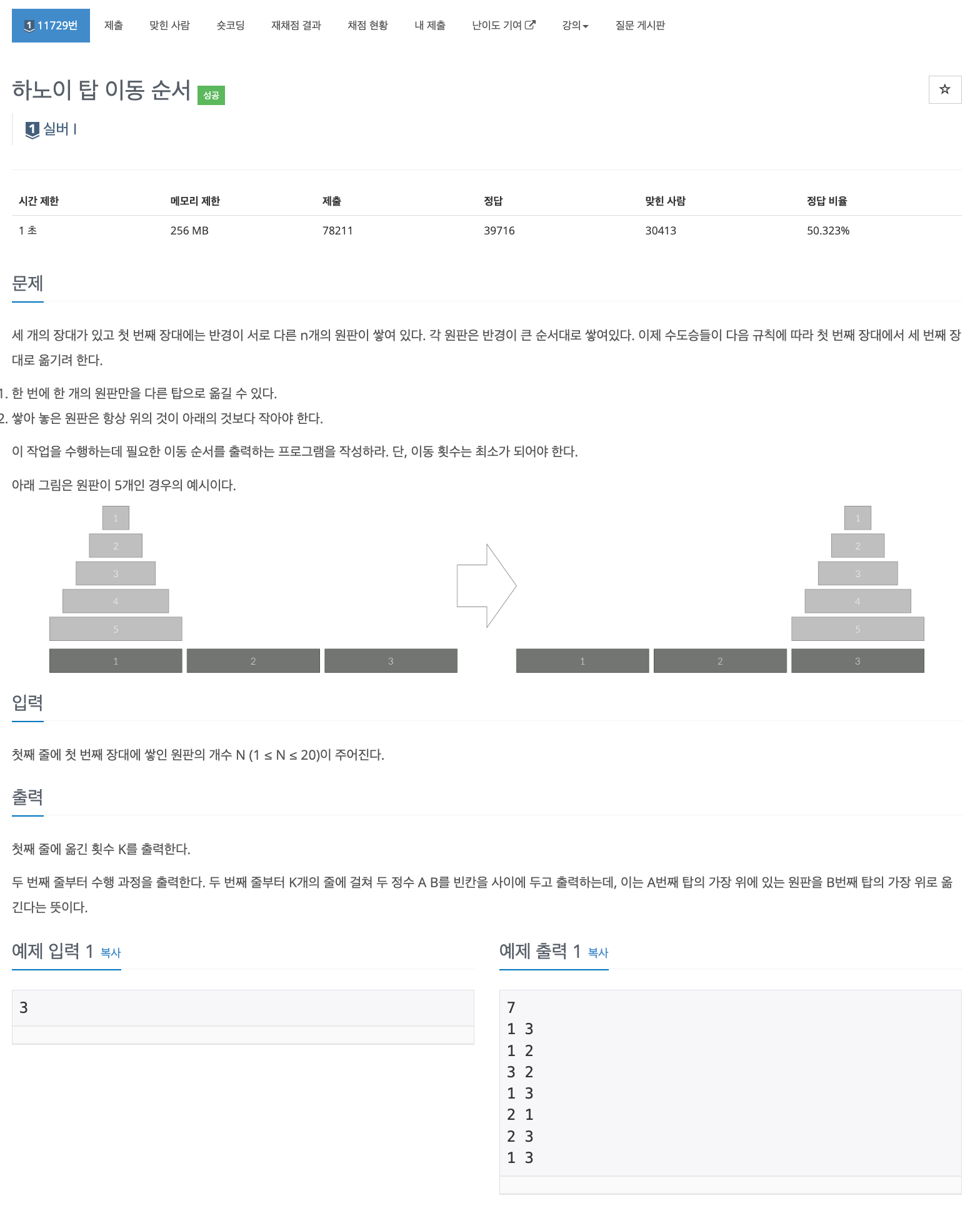
- 1번에 쌓여있는 원판들을 3번까지 옮겨야한다.
- 1회에 한 개의 원판만 옮길 수 있다.
- 반드시 큰 원판 위에 작은 원판이 있어야한다.
이 세가지 조건을 부합하여 문제를 살펴보자.
- 1번에 있는 가장 큰 원판을 3번으로 옮기기 위해서는 n-1개의 원판이 1번 -> 2번으로 가야한다.
- 1번에서 2번으로 가는 것을 hanoi함수로 정의한다면 hanoi(n-1)이 된다.
- 그 후 1번의 가장큰 원판이 3번으로 이동한다.
- 그렇다면, 이동횟수는 +1이 된다.
- 2번에 있는 (n-1)개의 원판이 3번으로 이동하기 위해서는 다시 hanoi(n-1)이 된다.
그렇다면 hanoi(n) = 2 * hanoi(n-1) + 1로 표현할 수 있다.
다음 위 수식을 보고 아래의 코드의 주석을 살펴보자.
정답 코드
import java.io.*;
public class Main {
static int count;
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine()); //원판의 개수를 입력
hanoi(N,1,2,3); //하노이 함수 실행
System.out.println(count);
System.out.println(sb);
}
static void hanoi(int N, int from, int temp, int to){ //파라미터로 N,from,temp,to를 입력받는다.
count++; //하노이 함수가 실행될 때마다 count +1
if(N == 1){ //만약 N이 1일 경우 출력문 추가 후 메서드 탈출
sb.append(from+" "+to).append('\n');
return;
}
hanoi(N-1,from,to,temp); //n-1개를 1번에서 2번기둥으로 옮긴다.
sb.append(from+ " " + to).append('\n');//1번기둥에는 가장큰 원판만 남음으로 출력
hanoi(N-1,temp,from,to); //n-1개를 2번기둥에서 1번기둥으로 옮긴다.
}
}
정리
그리 어렵지 않은 문제임에도 불구하고.. 재귀만 나오면 머리가 아프다..
함수 종료조건, 문제 정의하기 등 다양한 방법이 있지만.. 아직 와닿지는다..
하지만 계속해서 학습해나가다 보면 왕도가 보일 것이라고 생각한다..!