[백준] 17103번-골드바흐 파티션-Java

13 Jun 2023 in Algorithm on Algorithm

[백준] 17103번-골드바흐 파티션-Java

---

❓문제

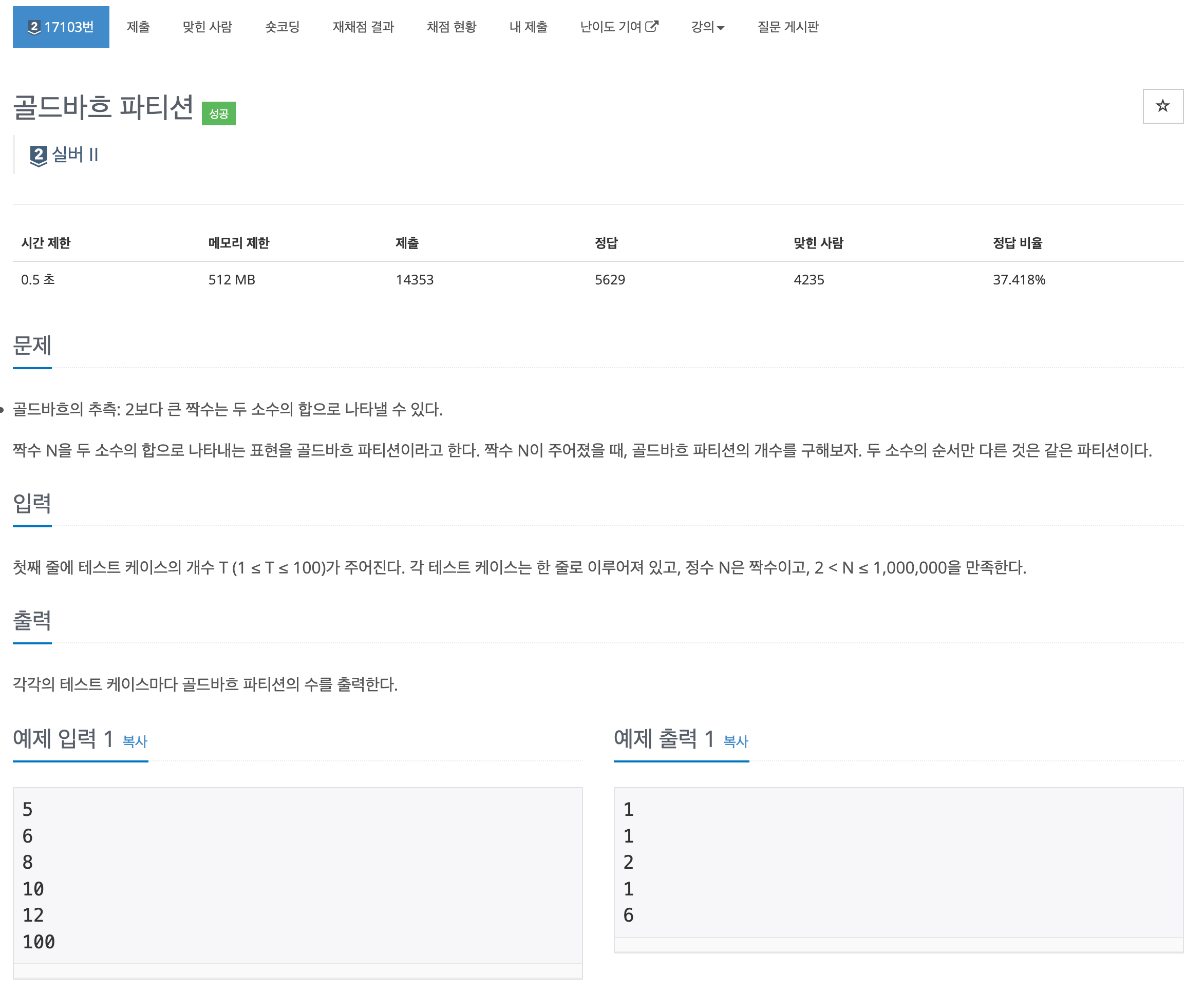
1. 골드바흐의 추측 : 2보다 큰 짝수는 두 소수의 합으로 나타낼 수 있다.
2. 테스트 케이스의 개수 T와 각각의 케이스만큼의 N이 입력되었을 때 골드바흐 파티션의 개수를 구하라.
   • 예시 : 4 -> 2+2로 1가지, 10-> 3+7, 5+5로 2가지
   • 단, 3+7과 7+3의 케이스와 같이 두 소수의 순서만 다른 것은 같은 파티션으로 간주한다.

T, N의 범위

1 ≤ T ≤ 100 2 ≤ N ≤ 1,000,000

🖊️풀이법

N의 범위가 최대 1,000,000까지만 소수를 찾으면 되기 때문에 크기가 1,000,001의 boolean타입의 배열을 만들어 푼다.

1. 소수를 검증할 크기가 1,000,001인 boolean[] prime을 생성
2. 해당 prime배열의 인덱스 값이 소수인지 아닌지 검증하는 메서드 구현 및 실행
3. j가 1씩 증가하는 N/2 만큼의 반복문을 순회하며, N - j 의 값과 j가 모두 소수(false)일 경우 count를 1씩 증가
4. 각각의 케이스의 count값을 출력한다.

정답 코드

import java.io.*;


public class Main {
    public static void main(String[] args) throws IOException {
        boolean[] prime = new boolean[1000001];
        isPrime(prime);
        prime[0] = prime[1] = true;
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        int T = Integer.parseInt(br.readLine());
        for (int i = 0; i < T; i++) {
            int N = Integer.parseInt(br.readLine());
            int count = 0;
            for(int j = 2; j <= N/2; j++){
                int tmp = N - j;
                if(!prime[tmp] && !prime[j]){
                    count++;
                }
            }
            sb.append(count).append('\n');
        }
        System.out.println(sb);
    }
    static void isPrime(boolean[] prime) {
        for (int i = 2; i < Math.sqrt(prime.length); i++) {
            if (prime[i]) {
                continue;
            }
            for (int j = i * i; j < prime.length; j += i) {
                prime[j] = true;
            }
        }
    }
}

---

정리

이번 문제는 간단한 소수를 구하는 알고리즘을 활용하는 문제이다.
해당 문제 또한 소수값을 구해야하는 범위의 최대치가 지정되어있어 하나의 boolean[]을 사용하여, 풀면 효율적이다.
또한 10의 테스트 값이 주어졌을 때, 3과 7, 7과 3은 동일한 케이스로 굳이 10의 반복문을 순회할 필요하없이 N/2번의 반복문만 순회하는 효율적인 로직을 작성할 수 있다.